
The Andrew and Erna Viterbi Faculty of Electrical & Computer Engineering
Technion – Israel Institute of Technology, Haifa 32000, Israel
E-mail: fischer@ee.technion.ac.il
Homepage: https://fischer.net.technion.ac.il
Wikipedia: In English, In Hebrew
Tel: +972-4-8294736 (office); +972-525345365 (mobile); +972-4-8325427 (home)
Office: Room 667, Mayer (EE) Building
Links to related Technion sites:
- Technion
- The Andrew and Erna Viterbi Faculty of Electrical Engineering, Technion
- Group Research Lab: Harry Stern Nonlinear-Optics Lab
- The Barbara & Norman Seiden Optoelectronics Center
- The Sara & Moshe Zipsapel Nano-Electronics Center
- The Lord Wolfson Micro-Electronics Center
Some of our recent work and papers:
[See in Research highlights #27 and #18 two QUESTIONS (“WHY…?”) with explanations.]
- Bose-Einstein condensation (BEC) of photons in fiber cavities
“Bose-Einstein condensation (BEC) of photons in an Er-Yb co-doped fiber cavity”. Nature Comm. 10, 747 (2019) or Nature Comm. 10, 747 (2019); Supplementary Information for the paper (Nature Comm. 10, 747 (2019).
and “Bose-Einstein condensation (BEC) of photons in a long fiber cavity”. Opt. Express 29, 27807 (2021), or in pdf Opt. Express 29, 27807 (2021).
Bose-Einstein condensation (BEC) was predicted in 1924-5 but it took 70 years to experimentally observe it. Such condensates, with a large portion of the particles occupying the ground-state at a nonzero temperature, were considered a new form of matter, a “quantum phase“, where the quantum regime covers many particles and rules their overall wave-function. BEC was experimentally demonstrated in 1995 by two groups with bosonic atoms at ultra-low temperatures of a few hundred nano-Kelvin (and therefore system cost of many million Dollars). They were awarded for this observation the 2001 Nobel Prize in Physics.
We recently demonstrated (Nature Comm. 10, 747 (2019), and Opt. Express 29, 27807 (2021)) quantum-based BEC of photons in a standard one-dimensional (1D) erbium-ytterbium co-doped fiber cavity at, below and above room temperature (cost of a few hundred Dollars). Photons are bosons, but usually their number is not conserved and therefore they have a zero chemical potential that cannot yield BEC. However, it can be different in some cases of cavities with gain and low photon loss-rates, as it is in our fiber system. The first paper (Nature Comm. 10, 747 (2019)) uses the standard linear dispersion relation in fibers and the BEC is based on a finite fiber cavity size effect in 1D. The second paper (Opt. Express 29, 27807 (2021)) uses a special sublinear dispersion and therefore the photon-BEC there is valid also in the long fiber cavity limit.
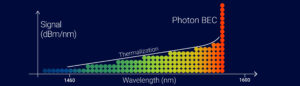
- Thermalization of one-dimensional photon gas and thermal lasers in erbium-doped fibers
Opt. Express 25, 18963 (2017) or in pdf: Opt. Express 25, 18963 (2017) .
Supplementary Video on the spectrum evolution of photon thermalization in an open erbiun-doped fiber
“Breaking two laser axioms: Lasing without an overall inversion and thermal equilibrium”: Paper 102, arXiv 1607 01681 (2016) (v. 1) or arXiv 1607 01681 (2016) (v.2), or in pdf: arXiv (v. 2).
We found spectra that have not been seen yet in light gain media such as the probably most frequently used one, erbium-doped fiber (edf). Our observation differs from the commonly accepted view that photons in lasers are not in thermal equilibrium, and don’t show Bose-Einstein spectral distribution and Bose-Einstein condensation (BEC). We show thermalization of photons in standard one-dimensional (1D) edf cavities and even in open edf, and unusual Bose-Einstein spectra in a range that reach ~200 nm, and lasing without an overall inversion.
- Unusual (sub-linear) light dispersion in fibers
The light dispersion relation is commonly linear or close to linear in complex refractive media in regions far from resonances, and therefore the frequency mode spacing there is uniform or close to uniform. We analytically and experimentally study chirped gratings based Fabry-Perot that gives at the 1550nm wavelength regime sub-linear dispersion (in the experiment a square-root dependence), and therefore a nonuniform comb structure and a density of mode states with a nonzero exponent as required, for example, for BEC in one-dimension (1D).
“Nonlinear light mode dispersion and nonuniform mode comb by a Fabry-Perot with chirped fiber gratings”,
Opt. Express 28, 18135 (2020); or in pdf: Opt. Express 28, 18135 (2020).
- Tuning, selecting and switching wavelengths in lasers with chirped fiber Bragg gratings (CFBGs) by high-order mode-locking
A new tunable laser based on a concept of cavity resonance activated wavelength selection (CRAWS) in mode-locked lasers.
Opt. Comm. 431, 151 (2019) (See also Patents 7, 9)
With Supplementary data there of:
Video S1. Continuous wavelength tuning in a range of 17.5 nm showing the optical spectra and the temporal waveforms (at the bottom left side) as the modulation frequency is continuously varied near 10 GHz.
Video S2. Continuous wavelength tuning in a range of 16.3 nm showing the optical spectra and the temporal waveforms (at the bottom left side) as the modulation frequency is continuously varied near 25 GHz.
- Bistability in a ring erbium-doped fiber laser due to ejected backward amplified spontaneous emission
Opt. Express 25, 32541 (2017) or in pdf: Opt. Express 25, 32541 (2017)
- Noise-mediated Casimir-like pulse interaction
Optica 3, 189(2016) or in pdf: Optica 3, 189(2016), Supplementary Information.
We present a new universal interaction mechanism between pulses mediated by noise in multi-pulse passively mode locked laser cavities. The interaction arises because of the suppression of the fluctuations of the radiation field, as does the attraction of conductors in the Casimir effect in quantum electrodynamics.
- CW (classical) laser condensation
Opt. Express 24, 6553 (2016) or in pdf Opt. Express 24, 6553 (2016)
We present a first experimental demonstration of classical CW laser light condensation (LC) in the frequency (mode) domain that verifies its prediction (Fischer and Weill, Opt. Express 20, 26704 (2012)). LC is based on weighting the modes in a noisy environment in a loss-gain measure compared to an energy (frequency) scale in Bose-Einstein condensation (BEC). It is characterized by a sharp transition from multi- to single-mode oscillation, occurring when the spectral-filtering (loss-trap) has near the lowest-loss mode (“ground-state”) a power-law dependence with an exponent smaller than 1. An important meaning of the many-mode LC system stems from its relation to lasing and photon-BEC.
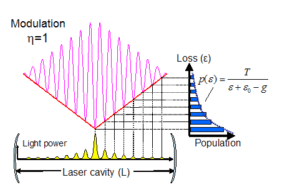
- Classical condensation of light pulses in a loss trap in a laser cavity
Optica 1, 145 (2014) or in pdf: Optica 1, 145 (2014)
We propose and experimentally demonstrate classical condensation of pulses in a loss-trap that is similar to Bose-Einstein condensation (BEC) of bosons in a potential-trap, but classical (and not quantum). The pulses and their loss levels serve as the particles and the energy levels, and the noise-induced power distribution replaces the quantum-thermal Bose-Einstein statistics. It is done by applying on the pulse system an envelope modulation that produces a loss-trap. Like BEC, classical pulse-condensation depends on the trap exponent.


- Many-Body Photonics
Optics & Photonics News (OPN) 24, 40 (2013) – September issue or PDF from Technion or OPN Digital
The full OPN September 2013 issue or OPN Digital or PDF
 Statistical mechanics is key to understanding thermodynamic systems, but most people don’t think of it as a tool for describing what goes on in photonics. Baruch Fischer begs to differ. “Adding many-body physics to photonics is challenging and rewarding,” he said. “How otherwise can one deeply understand, for example, laser mode-locking and the role of noise there? It would be like being limited to watching the world around 0 K— frozen in an ice age with no water and no melting.”
Statistical mechanics is key to understanding thermodynamic systems, but most people don’t think of it as a tool for describing what goes on in photonics. Baruch Fischer begs to differ. “Adding many-body physics to photonics is challenging and rewarding,” he said. “How otherwise can one deeply understand, for example, laser mode-locking and the role of noise there? It would be like being limited to watching the world around 0 K— frozen in an ice age with no water and no melting.”
Our first papers on the subject:
Theory: Phys. Rev. Lett, 89, 103901 (2002), Optics Comm. 223, 151 (2003),
Experiment: Opt. Express 11, 3418 (2003), or 57.
- Laser mode hyper-combs
Opt. Express 21, 6196 (2013) or in pdf: Opt. Express 21, 6196 (2013)
A rare physical realization of the “Spherical-Model” by a one-dimensional mode-locked laser system that is mapped to any (synthetic) dimension, even higher than 3, of the Spherical-Model, originally presented as a unique, but not realistic, many-body interacting magnetic spin system model that is analytically solvable in any dimension.
- When does single-mode lasing become a (classical) condensation phenomenon? (… to BEC or not to BEC of photons in optical cavities?)
Opt. Express 20, 26704 (2012) or in pdf: Opt. Express 20, 26704 (2012)
arXiv: 1207.2712 [physics.optics; cond-mat.stat-mech], (2012) arxiv.org/abs/1207.2709v2
- Laser light-mode (classical) condensation in actively mode-locked lasers
(A classical effect but formally similar to Bose-Einstein condensation – BEC):
Theory : Phys. Rev. Lett. 104, 173901 (2010)
Experiment: Opt. Express, 28, 16520 (2010) or in pdf: download from Technion
Pulse condensation in an AML laser cavity occurring for modulation (“potential trap”) exponents eta<2):
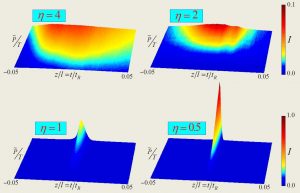
Hearsay on our theoretical laser BEC work: “Mode-locked lasers – Light condensation“,
by A. Fratalocchi in News & Views of Nature Photonics, 4, 502 (2010)
- Critical Behavior of Light in Mode-Locked Lasers:
Theory: Phys. Rev. Lett. 95, 103903 (2005) .
Experiment: Phys. Rev. Lett. 105, 013905 (2010)
Videos: A light-pulse tour on the slopes of the phase diagram (experiment),
shown in two parts:
The videos show experimental pulse waveforms formed in a mode-locked laser as they vary along two paths in the phase diagram: One path passes a discontinuous first order phase transition between the “para-pulse and “spontaneous-pulse” phases, and the second is near the critical point.

- Experiments showing how pulses are formed and annihilated in a passively mode-locked laser as a cascade of first order phase transitions:
Paper: Phys. Rev. Lett. 93, 153901 (2004)
Videos: Pulses formation (experiment)
Pulses annihilation (experiment)
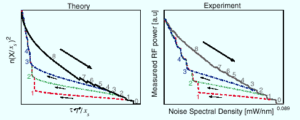 The movies show pulses generation in the experiment with the corresponding order parameter(via output pulse detection and RF power meter) as the noise power (“temperature“) is varied.
The movies show pulses generation in the experiment with the corresponding order parameter(via output pulse detection and RF power meter) as the noise power (“temperature“) is varied.
Typical pulse width is ~500 femto-sec. The pulse bunch length is ~1/300 of the cavity length.
Mode-locking can generate close to ~2 femto-sec (~2´10-15sec) pulses.
- Mode-locking as a phase transition globally solved for any laser parameters:
Paper: Phys. Rev. Lett. 97, 113902 (2006)
- A non-Optic work:
The Distribution Route from Ancestors to Descendants:
Paper (in Hebrew): “על פילוג צאצאים במהלך הדורות“, B.D.D. (Bar-Ilan Univ. Press), 23, 71 (2010)
